In mathematics, the order of operations is frequently used to solve mathematical expression problems in an accurate way. PEMDAS or BODMAS tells the correct way to solve arithmetic operations like plus, minus, multiply, or divide.
This technique is used all over the world to get similar and accurate results for math expression problems. In this post, we will study different rules to solve math expressions accurately.
Order of operations
In mathematics, the order of operations is an order that is used to solve the expressions of mathematics. It is the order in which the arithmetic operations like sum, difference, product, & quotient, brackets, and exponent operations are solved in a well-known sequence.
The two worldwide rules of this technique are:
1. PEMDAS2. BODMAS
The PEMDAS rule is mainly used in Western countries like the US, UK, Canada, etc., while the BODMAS rule is used in Asian countries like India, Pakistan, Sri Lanka, etc. Let’s study the BODMAS and PEMDAS rules briefly.
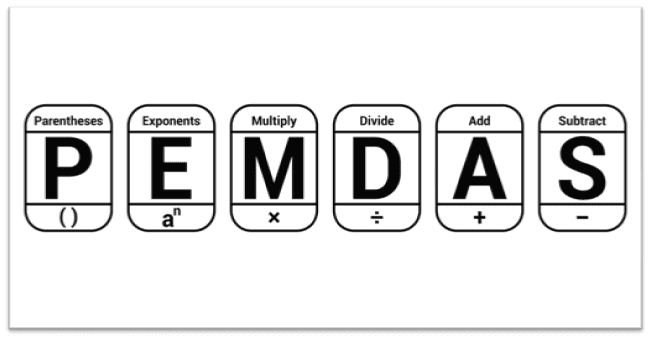
(i) PEMDAS Rule
The well-known and worldwide rule of the order of operations is said to be the PEMDAS rule. The word PEMDAS stands for Parentheses “()”, Exponent “^”, Multiplication “*”, Division “/”, Addition “+”, and Subtraction “-”.
Follow the steps below to solve the math expression according to the PEMDAS rule.
1. First of all, solve the parentheses present in the given math expression. If there is more than one parenthesis, then solve the leftmost parenthesis first.
2. After solving the parentheses, solve the exponent terms present in the math expression. If there is more than one exponent, then solve the leftmost exponent term first.
3. Then solve the product and quotient of the math expression from left to right.
4. In the end, solve the addition and subtraction operations from left to right.
Example: By the PEMDAS rule
Solve 32 + (12 – 2) + 62 – 20/2 + (3 + 17) – 5 (6 * 4) * 4 by using the PEMDAS rule.
Solution
Step I: Write the given math expression.
32 + (12 – 2) + 62 – 20/2 + (3 + 17) – 5 (6 * 4) * 4
Step II: First of all, solve the parentheses present in the given math expression.
32 + (10) + 62 – 20/2 + (3 + 17) – 5 (6 * 4) * 4
32 + 10 + 62 – 20/2 + (20) – 5 (6 * 4) * 4
32 + 10 + 62 – 20/2 + 20 – 5 (24) * 4
32 + 10 + 62 – 20/2 + 20 – 120 * 4
Step III: Now solve the exponent terms present in the given math expression.
(3 x 3) + 10 + 62 – 20/2 + 20 – 120 * 4
9 + 10 + 62 – 20/2 + 20 – 120 * 4
9 + 10 + (6 x 6) – 20/2 + 20 – 120 * 4
9 + 10 + 36 – 20/2 + 20 – 120 * 4
Step IV: Now solve the multiplication and division terms from left to right.
9 + 10 + 36 – 20/2 + 20 – 120 * 4
9 + 10 + 36 – 10 + 20 – 120 * 4
9 + 10 + 36 – 10 + 20 – 480
Step V: Solve the addition and subtraction terms from left to right.
9 + 10 + 36 – 10 + 20 – 480
19 + 36 – 10 + 20 – 480
55 – 10 + 20 – 480
45 + 20 – 480
65 – 480
-415
Step VI: Write the given math expression with the result.
32 + (12 – 2) + 62 – 20/2 + (3 + 17) – 5 (6 * 4) * 4 = -415
To avoid such a large number of steps to solve the math expression, use an order of operations calculator.
(ii) BODMAS Rule
The BODMAS rule is another well-known rule to solve math expressions accurately. This rule stands for Brackets (brackets can be braces or parentheses), Order of (exponent “^”), Division “/”, Multiplication “x”, Addition “+”, and Subtraction “-”.
Follow the steps below to solve the math expression according to the BODMAS rule.
1. First of all, solve the brackets, parentheses, and braces present in the given math expression. If there is more than one pair of parentheses or braces, then solve the leftmost pair of parentheses or braces first.
2. After solving the brackets, parentheses, or braces, solve the order of the terms present in the math expression. If there is more than one exponent, then solve the leftmost exponent term first.
3. Then solve the division and multiplication terms of the math expression from left to right.
4. In the end, solve the addition and subtraction operations from left to right.
Example: By the BODMAS rule
Solve 62 + (8 – 2) * 2 + 42 – 30/2 + (13 + 17) – 5 (12 * 4) / 6 by using the BODMAS rule.
Solution
Step I: Write the given math expression.
62 + (8 – 2) * 2 + 42 – 30/2 + (13 + 17) – 5 (12 * 4) / 6
Step II: First of all, solve the parentheses present in the given math expression.
62 + (8 – 2) * 2 + 42 – 30/2 + (13 + 17) – 5 (12 * 4) / 6
62 + (6) * 2 + 42 – 30/2 + (13 + 17) – 5 (12 * 4) / 6
62 + 6 * 2 + 42 – 30/2 + (30) – 5 (12 * 4) / 6
62 + 6 * 2 + 42 – 30/2 + 30 – 5 (48) / 6
62 + 6 * 2 + 42 – 30/2 + 30 – 240 / 6
Step III: Now solve the exponent terms present in the given math expression.
62 + 6 * 2 + 42 – 30/2 + 30 – 240 / 6
(6 x 6) + 6 * 2 + 42 – 30/2 + 30 – 240 / 6
36 + 6 * 2 + (4 x 4) – 30/2 + 30 – 240 / 6
36 + 6 * 2 + 16 – 30/2 + 30 – 240 / 6
Step IV: Now solve the division and multiplication terms from left to right.
36 + 6 * 2 + 16 – 30/2 + 30 – 240 / 6
36 + 12 + 16 – 30/2 + 30 – 240 / 6
36 + 12 + 16 – 15 + 30 – 240 / 6
36 + 12 + 16 – 15 + 30 – 40
Step V: Solve the addition and subtraction terms from left to right.
36 + 12 + 16 – 15 + 30 – 40
48 + 16 – 15 + 30 – 40
64 – 15 + 30 – 40
49 + 30 – 40
79 – 40
39
Step VI: Write the given math expression with the result.
62 + (8 – 2) * 2 + 42 – 30/2 + (13 + 17) – 5 (12 * 4) / 6 = 39
Summary
In this post, we have discussed all the basics of the order of operations along with its rules and examples. Now, after reading the above post, you can solve any math expression problems easily and accurate way.










No comments: